Note-A-Rific: Elastic Potential Energy

---

Any object than can be deformed (have its shaped changed) and then return to its original shape can store elastic potential energy.

· We’re still talking about potential energy, since it is stored energy until the object is allowed to bounce back.

· “Elastic” does not refer to just things like elastic bands…other materials that would be referred to as elastic would be

o pole vaulter’s pole

o springs

o cheese (no, I’m just kidding. Just wanted to see if you’re paying attention)

You learned in Physics 20 that Hooke’s Law is…

F = kx

F = force (N)

k = spring constant for that object (N/m)

x = amount of expansion or compression (m)

We can use this formula to figure out a formula for the energy stored in the spring.

· Remember that W = F d

· We might be tempted to just shove the formula for Hooke’s Law into this formula to get W = kxd = kx², but this is wrong!

· You have to take into account that the force is not constant as the object returns to its original shape… it’s at a maximum when it is deformed the most, and is zero when the obect is not deformed.

· Let’s graph Force vs Distance of Expansion for a spring that was stretched and we are now letting go of it…

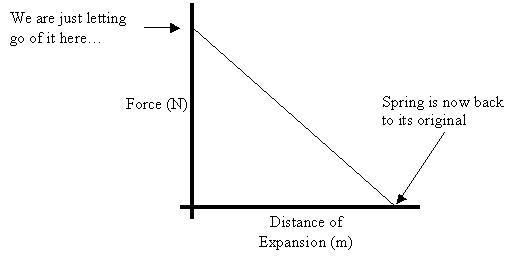
But this is really just a Force vs Displacement Graph like the ones we just looked at a couple of sections back! To figure out the energy of the spring we can just figure out the work it does by looking at the area under the graph.

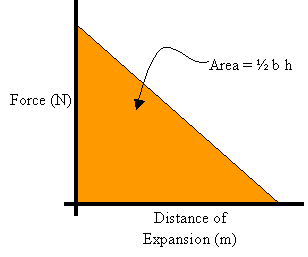Area = ½ bh

= ½ F x

= ½ (kx) x

Area = ½ kx² = W

So the work done by the spring (and then energy it stored) can be calculated using…

E_e = ½ kx²

E_e = eleastic potential energy (J)

k = spring constant (N/m)

x = amount of expansion or compression [deformation] (m)

Example: How much energy does a spring with a k constant of 15 N/m store if it is stretched by 1.6m?

E_e = ½ kx²

= ½ (15N/m) (1.6 m)²

E_e = 19 J