Note-A-Rific: 2-D Collisions

---

We now need to turn our attention towards questions involving objects that collide in two dimensions.

· In the previous section we were looking at only linear collisions, which are quite a bit simpler (mathematically) to handle.

· Now we need to figure out some ways to handle calculations in more than one dimension.

· You actually learned about this in Physics 20 in the vectors section.

· Anytime you see anything in a question about angles, you must not use the calculation methods you used in the 1-D conservation of momentum questions!

There are two different ways of handling these problems, and it depends on how comfortable you are with different mathematical ways of handling vectors.

· Sometimes one method may be better than the other for a particular problem, but try to become comfortable with one of the methods and then try to work out problems that way.

First, let’s look at a situation where only one object is moving at the beginning, then collides with a second stationary object…

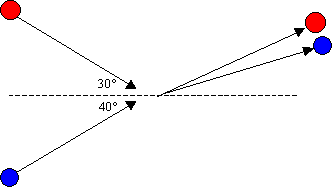
Example 1: A red ball with a mass of 15.0kg is moving to the right at 4.00m/s. It has a glancing collision with a stationary 10.0kg blue ball. After the collision the red ball is moving at 2.30m/s at an angle of 30° up from the horizontal. What is the velocity of the blue object now?

Notice that the word “glancing” is used in the question. Watch for words like this as a hint that it will be a 2-D collision.

We should draw a diagram of the situation to make sure that we know what is going on. Even if you feel certain that you know everything about 2-D collisions, always draw a quick sketch.

o We will assume that the blue ball moved downwards after it was hit… it just makes sense that it would move that way. We’ll figure out its exact angle later.

Now let’s look at this in terms of conservation of momentum…

o Initially, the only object that’s moving is the red ball. The red ball has all of the initial momentum.

o After the collision, both the red and blue ball are moving, so both of them have momentum.

o This means that the original momentum of the red ball (initial momentum) must equal the red plus blue balls momentum after the collision (final momentum).

o This is still like 1-D collisions, in that the momentum before must equal the momentum after.

o What we need to take into account now are the angles, and there are two methods to do this.

Method 1: Component Method

This is probably the more popular method, because it looks like the way most people learn about vector addition in Physics 20.

o We will break up each vector into x and y components, then add them up, and then figure out a resultant.

o The key to this method is that the total of all the y components before is equal to the total of all the y components after, and the total of all the x components before is equal to the total of all the x components after

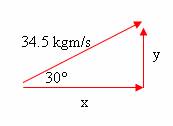
o We will first look at the components of the initial momentum (it’s the easy one!)

Initial Momentum Components…

There’s only one! The red ball is the only object moving at the start, and it is moving completely horizontally. That means it has no y-component, only an x component.

Red Ball’s Components

y = 0 kgm/s

x = 60 kgm/s

Totals

y_total = 0 kgm/s

x_total = 60kgm/s

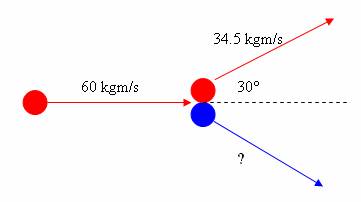
Final Momentum Components…

This one’s more complicated. What we know is that the total y and x components from above will still be the same

Totals

y_total = 0 kgm/s

x_total = 60kgm/s

Red Ball’s Components	Blue Ball’s Components
Use regular trig (since this is a 90° triangle) to figure out the x and y components. We will say that the x and y components are both positive (they’re pointing to the right and up).	First we will figure out the components of the blue ball, then we can calculate its resultant velocity. Remember that the totals shown above have to stay the same. Also, the y component on this diagram is negative since it is pointing down.
y = 17.3 kgm/s x = 29.9 kgm/s	y = -17.3 kgm/s (since the total must be “0” and the red ball is +17.3 kgm/s) x = 30.1 kgm/s (since the total must be 60 kgm/s and the red ball was only 29.9 kgm/s)

Since we know the x and y components for the blue ball, we can calculate its resulatant momentum, its velocity, and the angle it was traveling at.

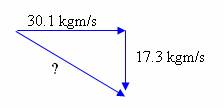
Notice that I didn’t bother putting the negative sign on the y component… it was just telling me that the arrow points down, which can be seen in the diagram.

c^2 = a^2 + b^2 c^2 = 30.1^2 + 17.3^2 c = 34.7 kgm/s

p = mv v = p/m = (34.7 kgm/s) / (10.0 kg) v = 3.47 m/s

tan θ = opp / adj = (17.3) / (30.1) tan θ = 0.573 θ = 29.9°

Final Answer: The blue ball will travel at 3.47 m/s at an angle of 29.9° below the horizontal.

Method 2: Sine and Cosine Law Method

This is the method that fewer people use, because they can be a bit intimidated by the math.

o If you are careful to set up the diagram properly, and carefully do the calculations, you’ll find that this method is often quicker for this sort of problem.

o You can really only use this method if one of the objects was initially at rest. Otherwise you can’t draw a proper triangle for a diagram (as you’ll soon see).

o Remember, the initial momentum of the ball (the red ball moving at first), must be equal to the final momentum (the two balls moving in the end).

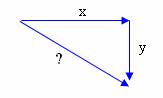
If we add the two final vectors (head-to-tail) we get this diagram…

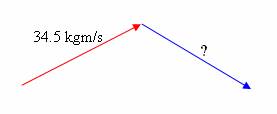
And then we remember that these two added together must equal the initial momentum; that means the initial momentum of the red ball must be the resultant in this diagram.

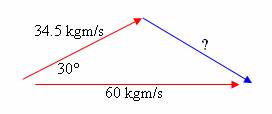
This is not a right angle triangle, so we can’t use regular trig. We can use cosine and sine laws, though.

o If you’re not familiar with them, I’d suggest you skip this part, and just use the component method. This isn’t necessarily the best place to learn a new hunk of math. Go ahead and try if you want…

c^2 = a^2 + b^2 – 2ab cos θ = 34.5^2 + 60^2 – 2(34.5)(60) cos 30° c = 34.7 kgm/s

p = mv v = p/m = (34.7 kgm/s) / (10.0 kg) v = 3.47 m/s

sin θ = sinβ a / b = sin 30° (34.7) / (34.5) θ = 30.2°

Final Answer: The blue ball will travel at 3.47 m/s at an angle of 30.2° below the horizontal.

Don’t worry too much about the slight difference in angles… rounding off can play nasty tricks ;)

Example 2: A moving 1.20 kg red ball strikes a stationary 2.31 kg blue ball. If the final velocity of the red ball is 13.5m/s at 23° above the horizontal, and the blue ball is moving at 4.59 m/s at 42° below the horizontal, what was the initial velocity of the red ball?

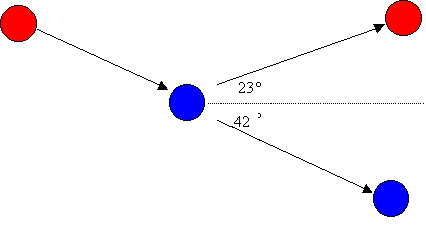
We’ll just try this example with components. If you want to try cosine/sine, go ahead.

First, we’ll just figure out the momentum of the balls on the paths they’re on…

p_r` = m<sub>r</sub>v<sub>r</sub>` = (1.2kg)(13.5m/s) = 16.2kgm/s

p_b` = m<sub>b</sub>v<sub>b</sub>` = (2.31kg)(4.59m/s) = 10.6kgm/s

Now, we can start breaking these values into x and y components. Start with the red ball…

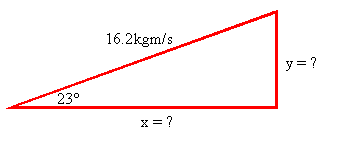
Just use regular sine, cosine, and tangent to figure out the x and y components.

You should get x_r = 14.9kgm/s and y_r = 6.33kgm/s .

Then do the same for the blue ball.

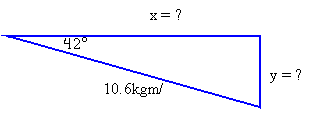
You should get x_b = 7.88kgm/s and y_b = 7.09kgm/s .

Both of the x components point to the right, so we can just go ahead and add them to get one big x component…

x_r + x_b = 14.9kgm/s + 7.88kgm/s = 22.8kgm/s

The red ball’s y component points up, but the blue ball’s points down.

· We’ll say that the one pointing up is positive, and the one pointing down is negative…

y_r + y_b = 6.33kgm/s + -7.09kgm/s = -0.76kgm/s

We now have a new triangle that we can make out of these new x and y components…

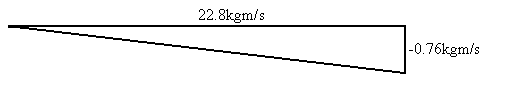
This represents the total momentum before and after the collision. Since only the red ball is moving before the collision, if we figure this out we will know the momentum of the red ball.

· Use Pythagoras to solve for the unknown side…

c² = a² + b²

c = 22.8kgm/s

· To determine the velocity of the red ball, use the momentum formula.

p = mv

v = p / m

= (22.8kgm/s)/(1.20kg)

v = 19m/s

· And use tangent to figure out the angle…

tanq = opp/adj

q = 1.9°

My final answer will be that the red ball is initially traveling at 19m/s at an angle 1.9° below the horizontal. It is important that you make a statement of your FINAL answer at the end of a problem like this, as you’ve probably been writing numbers all over the place.

Example 3: A 1.20 kg red ball moving at 10.0m/s strikes a 2.31 kg blue ball moving at 15.0m/s. If the final velocity of the red ball is 13.5m/s, what is the final velocity of the blue ball? Make use of the angles drawn in the following diagram.

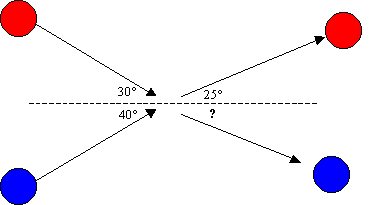
The total momentum of the balls before the collision is equal to the total momentum of the balls after the collision.

· We will calculate the total momentum of the red and blue balls before the collision by adding their components.

· This resultant is also the resultant of after the collision.

· We will use this, along with the components of the red ball after the collision to figure out the motion of the blue ball.

Do the red ball before the collision…

p_r = mv

= (1.20kg)(10.0m/s)

p_r = 12.0kgm/s

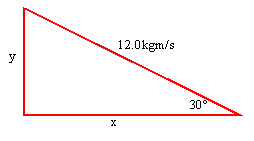
· Figure out the x and y components… you should get x = 10.4kgm/s and y = 6.00kgm/s.

Do the blue ball before the collision…

p_b = mv

= (2.31kg)(15.0m/s)

p_b = 34.7kgm/s

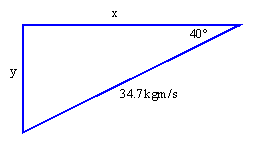
· Figure out the x and y components… you should get x = 26.6kgm/s and y = 22.3kgm/s.

We will now add the x and y components to get a new resultant.

· As before, the blue ball has a positive y component, but the red ball is negative, so we need to be careful.

· We can just go ahead and add the x components because they point in the same direction.

· After adding the x and y components you should have a new triangle like this.

Calculate the resultant and the angle. You might need it later, and it doesn’t take long to do…

· You should get 40.4kgm/s and 24°.

· Since this is a right angle triangle, the other angle is 66°, just in case you decide you need it later.

After the collision, all of the momentums have to add up to the same as the triangle drawn above.

· For this question I would suggest you start by calculating the components of the red ball’s momentum after the collision.

o Then you can figure out how much x and y component are “missing.”

o This must come from the blue ball!

The red ball after the collision…

p_r = mv

= (1.20kg)(13.5m/s)

p_r = 16.2kgm/s

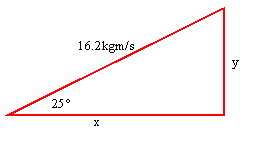
When you calculate the x and y components you should get x = 14.7kgm/s and y = 6.84kgm/s.

This means that there is a certain amount of x-component unaccounted for…

· 37.0kgm/s from the resultant

· Only 14.7kgm/s measured for the red ball

· 37.0kgm/s – 14.7kgm/s = 22.3kgm/s to the right

We also have some y-component unaccounted for…

· Although we originally assumed the blue ball would be moving down in our diagram, we now know that isn’t the case.

o The red ball had only 6.84kgm/s pointing up.

o According to our y-component from before the collision, we need 16.3kgm/s pointing up.

o So the blue ball must have an upward component of 9.5kgm/s upward.

Our blue ball has a diagram after the collision that looks like this…

· We calculate the hypotenuse as 24.2kgm/s.

o As the blue ball has a mass of 2.31kg, we can calculate the velocity of the ball as 10.5m/s.

o The angle is found to be 23° above the horizontal.

Our final answer is that the blue ball is moving at 10.5m/s at an angle of 23° above the horizontal after the collision.