Note-A-Rific: Elastic & Inelastic Collisions

---

We now know that momentum is conserved in collisions.

· This will hold true as long as the objects are an isolated system.

o This just means that no energy or matter is allowed to enter or leave the system.

If we are dealing with a collision involving really small objects (like atoms or molecules) you’ll often find that kinetic energy is also conserved.

· The total kinetic energy of all particles before the collision equals the total kinetic energy of all particles after the collision.

· If one particle “lost” some energy, it must have been picked up by another particle.

In every day collisions involving large objects like bowling balls and pins, it appears that kinetic energy is not being conserved.

· In these cases you’d probably measure that the kinetic energy after the collision is less than the kinetic energy before.

· The energy might have been “lost” in one of two ways…

1. Friction between the objects could cause some of it to be converted to heat (thermal energy).

2. If the object was permanently changed (broken, bent, snapped, twisted, etc.) from its original shape.

· Energy would have to be used to do this.

· If the change is very small (like two pool balls bouncing off of each other) than the “lost” energy is very small.

· If the change is big (a bowling pin shatters when hit by a bowling ball) the energy “lost” is great.

Quite often we will divide collisions into two groups, depending on whether or not energy was lost:

· Elastic Collision à Total kinetic energy before the collision equals total kinetic energy after.

· Inelastic Collision à The kinetic energy after the collision is less than before the collision. If the objects stick together after the collision, we say that the collision is completely inelastic.

If we know that a collision is elastic, we can use momentum and energy together to solve it, as the following example shows…

Example: The following diagram shows a small blue ball with a mass of 0.250kg moving at a velocity of 5.00m/s. It hits a 0.800kg red ball that is initially at rest. If the balls hit each other head on as an isolated system, and the collision is elastic, how fast are the balls going after the collision?

Since the collision has happened in an isolated system, momentum will be conserved.

p_total = p_total’

m_bv_b + m_rv_r = m_bv_b’ + m_rv_r’

Since the red ball isn’t moving before the collision…

m_bv_b + 0 = m_bv_b’ + m_rv_r’

We can’t use this formula to find v_b’ and v_r’ since we have two unknowns.

It is an elastic collision, so all kinetic energy is conserved.

E_{k total} = E_{k total} ‘

½ m_bv_b² + ½ m_rv_r² = ½ m_bv_b² + ½ m_rv_r²

Again, the red ball isn’t moving before the collision…

½ m_bv_b² + 0 = ½ m_bv_b² + ½ m_rv_r²

We now have two formulas with two unknowns. Try to solve them and reduce them to get something like…

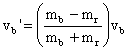
Substitute in your numbers and you’ll find that the blue ball is going at –2.62m/s (to the left) after the collision.

You can substitute that number back into one of the other formulas to find that the red ball is going at +2.38m/s (to the right) after the collision.

Einstein threw a monkey wrench in to the works when you are talking about moving objects and the energy the have.

· In his famous formula E = mc² he is basically saying that you can take the mass of an object and change it into energy… convert the entire object into pure energy.

o The “E” is energy measured in Joules, “m” is mass measured in kilograms, and “c” is the speed of light 3.0 x 10⁸m/s.

· This also implies that energy can be changed into mass!

· You don’t need to worry about doing anything with this in your calculations in Physics 30, but you do need to be aware of it.