Note-A-Rific: Momentum & Impulse

Momentum

Impulse

Newton

Graphing

Momentum

Momentum is an idea that is similar to inertia and kinetic energy.

Inertia is the property of an object to stay at rest or in motion.
Kinetic energy is the amount of energy that an object due to its motion. (E_k = ½ mv²)

· Momentum is calculated by multiplying the mass and velocity of an object.

p = m v

p = momentum (kg m/s)

m = mass (kg)

v = velocity (m/s)

Notice that momentum does not have a nice derived unit, although I would appreciate it if you lobbied physicists to name it the “Clintberg” in my honor. For now you’ll just need to give the units “kg m/s”

· If you compare and contrast momentum and kinetic energy (measured in Joules), you’ll notice a couple things…

o First, they both have mass and velocity in their formulas.

o Second, kinetic energy has to do with ability to do work, momentum doesn’t.

o Although they are similar, they are not the same.

We haven’t given you any way to calculated inertia yet, so is momentum the same as inertia?

Not really. Inertia is a concept, but not something that is directly measured.

Example: a) Which would you rather be hit by… a 1000 kg car moving at 10.0 km/h or a 0.50 kg ball moving at 10.0 km/h?

The easiest way to answer this is to calculate the momentum of the two objects.

Car

p = mv

p = 1000kg (2.78m/s)

p = 2.78 x 10³ kg m/s

Ball

p = mv

p = 0.5kg (2.78m/s)

p = 1.4 kg m/s

Obviously the car has more momentum (it also has more inertia). You’d probably be able to walk away after being hit by the ball, but you might find it a bit harder to walk away after the car.

b) How fast would the ball have to be moving to have the same momentum as the car?

p = mv à v = p/m = 2.78 x 10³ kgm/s / 0.50 kg = 5.5 x 10³ m/s = 20 000 km/h !!!

Impulse

· The simple definition for impulse is that it is a change in momentum.

· If an object’s velocity changes, there is a change in momentum, so there must be an impulse

· We assume that you are not going to change the mass of an object.

Dp = m Dv

Dp = impulse (change in momentum) (kgm/s)

m = mass (kg)

Dv = change in velocity (v_f – v_i) (m/s)

Example: A box of tic tacs (15g) is sliding along the table at 5.0m/s. I try to stop it, but only slow it down to 1.6 m/s. What impulse did I impart to the box?

Dp = m Dv

Dp = m (v_f – v_i)

= 0.015kg (1.6m/s – 5.0m/s)

Dp = -0.051 kg m/s

The negative sign just identifies that my impulse was in the negative direction.

But wait a second, if an impulse changes the velocity of the object, that means it’s accelerating.

· Acceleration of an object can only occur if a force is acting on the object… so force must be related to impulse in some way.

· This leads us to the link to Newton.

The tie-in to Newton…

When Newton came up with his 2^nd Law of motion, he didn’t write it in the form we usually see it today…

F = ma

· Remember that he was playing around with some new ideas, and didn’t necessarily look for the “easiest” way to state his theories.

· Instead, he kept talking about the “quantity of motion” of an object, what we today call momentum.

· When he stated his 2^nd law he said the force is proportional to the rate of change in the momentum.

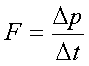
Notice that you can solve this formula to get what we now consider the “standard” form of the 2^nd law…

but we know that Dp = m Dv …

and we also know that …

\ F = ma

We can also come up with a different (and more versatile) version of the impulse formula.

· The formula you were first given was…

Dp = m Dv

· But we just saw that Newton used impulse in his formulas…

which becomes

Dp = F Dt (which can be a useful formula!)

· We can stick these two formulas together to get

FDt = mDv

You can see that a change in momentum (impulse) depends on two factors… force and time interval.

· To change an object’s momentum, think of the following situations:

1) You could apply a medium force over a medium time interval.

F Dt = Dp

2) You could apply a big force over a small time interval and get the same impulse as in (1).

F Dt = Dp

3) Or, you could apply a small force over a long time interval and still get the same impulse.

F Dt = Dp

This explains why you would want to come to a stop by hitting a haystack instead of a brick wall with your car.

· In each case the impulse is the same (your mass stays the same, your Dv stays the same).

· When you hit the brick wall…

F Dt = Dp

Youch! All that force on your body is going to hurt! The impulse happened in a very short time period.

· When you hit the haystack…

F Dt = Dp

Not much force at all, since the impulse is spread out over a long time period!

· It’s the force that “hurts”, so you want it to be as small as possible.

· You can use the same argument to explain hitting an airbag instead of a steering wheel.

Example: A 75kg man is involved in a car accident. He was initially traveling at 65km/h when he hit a large truck.

a) If he had no airbag in his car and he came to rest against the steering wheel in 0.05s, how much force was exerted on his body?

First, change 65 km/h into 18m/s.

FDt = mDv

F = (mDv)/ Dt

= (75kg)(-18m/s) / (0.05s)

F = -2.7 x 10⁴ N

a) If he did have an airbag that inflated and deflated correctly, bringing him to rest over a time of 0.78s, how much force was exerted on his body?

FDt = mDv

F = (mDv)/ Dt

= (75kg)(-18m/s) / (0.78s)

F = -1.7 x 10³ N

Which is only about 6% of the force felt without an airbag… a definite improvement!

Graphing Impulse

At times it can be useful to graph Force vs. Time to determine impulse.

What is the area under the graph?

Area = base X height

= F Dt

= Impulse

Example: I am in a car that is accelerating. I want to calculate the impulse that is acting on the car during this time of 5.78s. If I know that the force on the car increases from 0 N to 3012 N over this time, calculate the impulse.

Let’s start by graphing the information we were given…

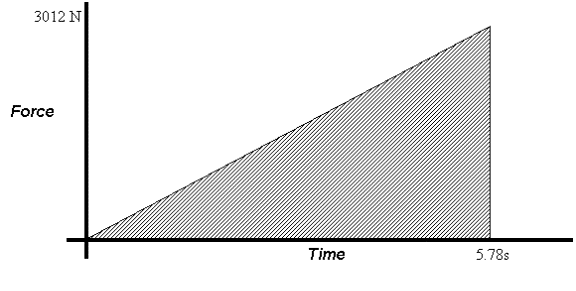
If we calculate the area under the graph (in this case a triangle) we will know what the impulse is.

A = ½ bh

= ½ (5.78 s)(3012 N)

A = 8.70 x 10³ kgm/s

Even if it is a curved line, you can still at least estimate the area under the graph…

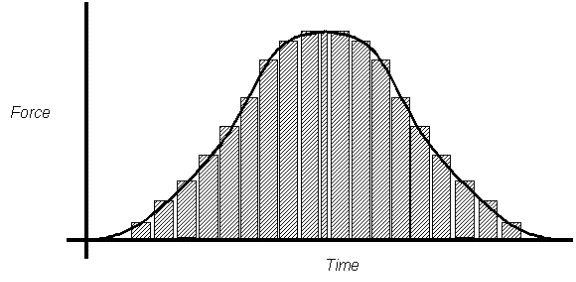
For a curved line like this one, we can figure out the area of a bunch of little columns under the line to approximate the true area.
If you’ve taken a calculus course then you’ll know that you can make better approximations by assuming an infinite number of columns under the line.
You are not responsible for calculus calculations in this course… we’d just want you to approximate the values as closely as possible.