Note-A-Rific: Electric Fields & Lines

Electric Fields

Just like gravity, the force due to electric charges can act over great distances.

·        But most forces we deal with in everyday life are “contact forces”… objects touch each other directly in order to exert a force on each other.

e.g. tennis racket hits a tennis ball

·        The idea of a force acting at a distance without direct contact was hard for early scientists, from Aristotle to Newton, to accept.

 

Then the British scientist Michael Faraday came up with the idea of a “field”.

·        A field is sometimes defined as a sphere of influence. An object within the field will be affected by it.

·        Two kinds of fields:

1.      Scalar Fields à magnitude but no specific direction

e.g. Heat field from a fire: If you stand by a campfire, you can measure the magnitude (temperature) of the field with a thermometer.

2.      Vector Fields à magnitude and direction

e.g. Gravity field: Measure acceleration towards the centre of an object.

·        We deal almost all the time with vector fields in Physics 30.

 

An electric field exists around any charge (positive or negative).

·        If one charge is placed near a second charge, the two fields will “touch” and exert a force on each other.

·        N.B. the field is NOT a force, but it does exert a force!

·        If you are pushing a box, I don’t say you are a force, but you are exerting a force.

 

How can we detect and measure the electric fields around charges?

·        Easiest way is to place another known charge near by and see how it reacts… but it has a field of its own, so that would affect your results.

·        Physicists have defined a “test charge” as being an infinitely small, positive charge.

·        It is a mathematical creation… they don’t really exist.

·        Since it is infinitely small, it has a minimal electrical field of its own.

·        Usually given the symbol q’ (q prime)

·        Since the test charge is positive:

·        if we see the test charge move towards the other charge we know that one must be negative

or

·        if the test charge moves away that one must be positive.

 

Remember, according to Coulomb’s Law, the force exerted on the test charge must be directly proportional to its own charge and the charge on the other object.

F a q1 q2  ß substitute the test charge in this relation

F a q’ q2

 

If you divide the force by the charge on the test charge, you get a new formula.

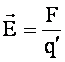
E = electric field (N/C)

(Arrow above “E” in formula shows this is a vector… it isn’t “energy” which is a scalar)

F = force (N)

q' = charge on test charge (C)

 

Example: I place a 3.7 C test charge 2.7m to the right of another charge. If there is an attractive force of 2.45N acting on the test charge, what is the field strength at that spot?

We don’t need the distance to figure this question out. It is important to know that the test charge is to the right of the other charge, since we need to give a direction.

E = F / q’ = 2.45N / 3.7C = 0.66 N/C [left]

The field points left because that’s the direction the test charge is being pulled.

 

Notice…

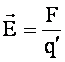        is the force per unit charge

 

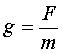         is the force per unit mass

 

è Gravity is a field also, a force acting at a distance ç

 

The direction of the field is always in the direction of the force on a positive test charge.

 

 

 

 

 

 

 

 

 


The electric field around a charge will be different at different locations around the charge.

1.      Further away from the charge, the magnitude of the force will decrease.

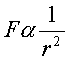
2.  Direction will be different.

 

 

 

 

 

 

 

 

 

 


Example 1: A force of 2.1 N is exerted on a 9.2 x 10-4 C test charge when it is placed in an electric field. If the force is pushing it West, what is the electric field at that point?

 

 

 

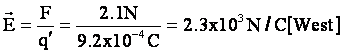
Example 2: If a positive test charge of 3.7 x 10-6 C is put in the same place in the electric field as in the last example, what force will be exerted on it?

 

è   F = E q = 2.3 x 103 N/C (3.7 x 10-6 C)

 

                                     F = 8.4 x 10-3 N  [West]

 

 

Since Coulomb’s Law is…

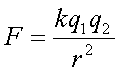
It can be substituted into the field formula to get…

 

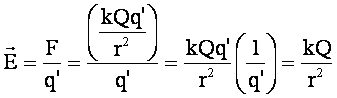
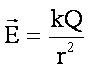
Super Important Note:

·        It is very important that you understand that in the example above the q’ is the little test charge, and Q is the charge producing the electric field.

·        It would be like doing an experiment to measure the gravity field on earth… m’ would be a little object you are dropping, and M is the mass of the earth, which is producing the gravity field.

·        So, in the formula above you will use the main, big charge that is actually producing the field you want to measure.

·        This is great! Now you don’t have to rely on some imaginary thing like a test charge to calculate the field around a regular charge!

 

·        Also notice that the formula  is very similar to the other gravity formula  from Physics 20.

 

Using this formula, if you know the charge on an object which is producing a field, and how far away you are from it, you can calculate the field at that point.

 

Example: A tiny metal ball has a charge of –3.0 x 10-6 C. What is the magnitude and direction of the field at a point, P, 30cm away?

 

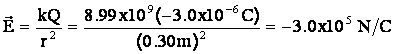
·        Since the electric field is always defined as being in the direction that a positive test charge would move, this field points towards the metal ball. That’s the direction you would state.

·        Get used to names for a particular spot like “P”, since sometimes we may want to relate what you’re doing in a question to several spots, like “P”, “D”, and “A”.

Field Lines

An electric field is a vector.

·        Therefore, we can represent an electric field with arrows drawn at various points around an object with charge.

·        These electric field lines (sometimes also called lines of force) are drawn below for two simple examples.

 

 

 

 

 

 

 

 

 

 

 

 

 


·        Notice that the lines are drawn to show the direction of the force, due to the electric field, on a positive test charge.

·        Also, the closer you get to the charge, the closer the lines are to each other.

o       This is where the electric field is getting stronger, which makes sense since you are closer to the charge.

o       If you pick a spot further out, you’ll see that the lines aren’t as dense there… so the field is weaker.

 

What would it look like if you had these two charges close enough to each other that their field lines could interact?

 

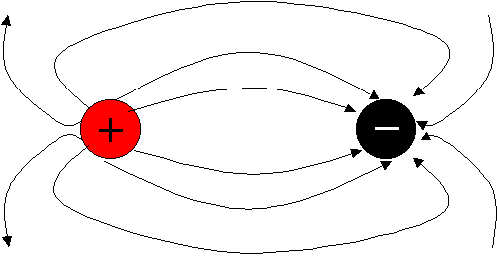
·        The arrows go from the positive charge to the negative charge.

·        The direction of the field at any point is the tangent drawn to the field line at that point.

 

Another important example of field lines comes out of the need to sometimes have a constant, uniform electric field.

·        As you can see in the example up above, the field has very different field strengths at different points… it’s irregular.

·        That’s because it is made up of only two charges, so the field lines wrap around a lot.

·        If we could get a whole bunch of charges lined up evenly then we could get a more uniform electric field.

·        It is possible to set this up using two plates that are parallel to each other with opposite charges built up on them.

 

 

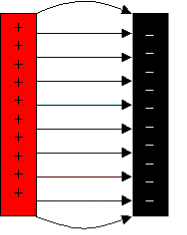
The field lines are very uniform all the way, except for a slight curvature at the ends.

·        We often ignore this slight curvature, since it is very small as long as the plates have a big surface area and are close together.

·        So, we can say that we have a constant electric field between these parallel plates.