Note-A-Rific: Franck-Hertz Experiment
Franck-Hertz Experiment
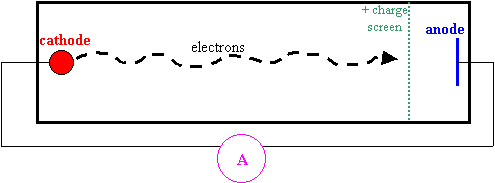
In 1914 James Franck and Gustav Hertz set up an apparatus to try to work out some of the mysteries that still surrounded the model of the atom that Bohr had proposed. They set up the following apparatus… (detailed diagram on page 839 in the text)
|
|
|
|
|
|
- Electrons are emitted from the cathode.
- A voltage that can be adjusted to increase the positive charge on the screen accelerates them, giving them kinetic energy.
- Most of the electrons easily pass through the screen and hit the anode… so the ammeter shows a current flowing.
- As the voltage is increased the current increases.
· Note: since we are accelerating electrons throughout this section, if a voltage is used to accelerate them they will gain energy that can be easily stated in electron volts (eV).
Example: An electron accelerated by 5.2V will have 5.2eV of kinetic energy.
Here’s the interesting part… fill up the tube with mercury vapour.
· They used mercury because they could easily put liquid mercury into the tube and let it evaporate into a gas once the tube was sealed.
· Now there’s something for the electrons to bump into.
· We would expect that not as many electrons will make it to the anode, so the current might drop off a bit.
 The
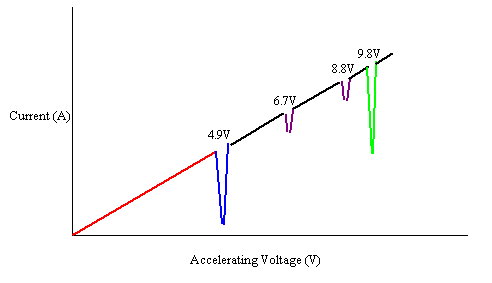
data they got is shown on this graph
The
data they got is shown on this graph
- As
the voltage increased increased from zero, the current steadily increased.
- At
4.9V (so each electron has 4.9eV of energy), the current dropped to nearly
zero (this means almost no electrons were getting to the anode).
- As soon as you passed 4.9V the current started going up again.
- There were two little drops at 6.7V and 8.8V, so at least some
electrons weren’t getting to the anode.
- At
9.8V there was one more big drop.
At first they weren’t sure how to interpret the information, but then they realised that if they took some of Bohr’s ideas and combined it with the quantum stuff, they might have a theory.
1. In the first section, nothing is happening that is different. If any of the electrons are hitting atoms of mercury, they must be bouncing right off and continuing. Mercury atoms will not absorb amounts of energy less than 4.9eV (sounds like quantum stuff to me!).
2. At 4.9eV, the mercury happily absorbs energy from electrons that hit it. Mercury will absorb this quantum of energy (4.9eV), this specific amount of energy. Since the mercury atom has absorbed exactly 4.9eV from the electron, the electron can’t go any further to the anode, so the current drops. Some electrons still sneak by without hitting mercury atoms, so we do get a little current still flowing.
3. For a while after 4.9eV, the mercury atoms will grab 4.9eV, but the electron still has enough energy to make it to the anode. For example, let’s say an electron has 6.0eV. It will hit a mercury atom (which absorbs 4.9eV) but it still has kinetic energy to continue moving (6.0 – 4.9 = 1.1eV).
4. At 6.7eV and 8.8eV, mercury will again absorb energy, but there is a smaller probability of it happening. It’s almost as if mercury will eat up those amounts of energy if it has to, but it doesn’t really like the flavour. So the drop in current isn’t as great.
5. Finally at 9.8eV, they figured out that two collisions must be happening. An electron is moving with 9.8eV of energy when it hits one mercury atom. The mercury atom absorbs exactly 4.9eV and the electron moves off with 4.9eV. Now the electron hits a second mercury atom which absorbs the remaining 4.9eV, leaving the electron with none.
What they had discovered is that atoms can change their internal energies by colliding with electons, but only in specific amounts… quanta!
- This internal energy is stored in electrons jumping up to higher excitation levels within the atom.
- Usually this energy is released again quite quickly as the electron drops back down to the ground state.
· This drop will release the energy out of the atom in the form of a photon.
It is common to draw on of the following diagrams to show the energies involved.
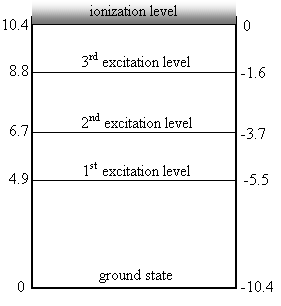
· Along the left side we have the energy (in eV) absorbed by the mercury atoms from electrons in a Franck-Hertz experiment
· Along the right side we have how much energy (in eV) the electron in the mercury atom is missing to be able to get out of the atom (this is like the way Bohr looked at hydrogen in the last section using negative values). This is the ionization level.
o At the ionization level the electron has gained so much energy that it flies out of the atom, leaving an ion behind.
|
|
|
|
|
|
Example: I apply a voltage of 7.0 V across a Franck-Hertz apparatus. What frequencies of EM will you see emitted by the mercury?
·
 We
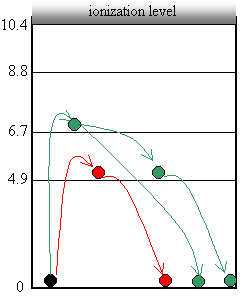
start with an electron at the ground state.
We
start with an electron at the ground state.
· Since I am applying 7.0V to the tube, there will be enough energy to knock electrons in the mercury up to the 1st and 2nd excitation levels.
· When that electron drops back down from the 1st level, it can only emit 4.9eV
o
E = hf à![]()
· When the electron drops back down from the 2nd level, it can do it in one big drop and release all of its 6.7eV.
o
E = hf à![]()
· The electron dropping down from the 2nd level might first drop down to the 1st level, so it only loses some of its energy.
o
E = hf à![]()
· Then that electron will drop from the first level to ground level, giving us a photon at 1.2 x 1015Hz (we calculated that one above).
· So, the final answer is that we will see frequencies of 1.2 x 1015 Hz, 1.6 x 1015 Hz, and 4.3 x 1014 Hz. These frequencies correspond to the release of 4.9eV, 6.7eV and 1.8eV.