Note-A-Rific:
Force on Wires
We saw in a previous section that a current in a wire can create a
magnetic field.
·
If
that wire has a magnetic field around it, it should feel a force if it is
brought near another magnet.
·
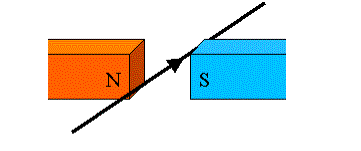
This
effect was shown by Oersted when he placed a current carrying wire into a
magnetic field and watched what happened.
·
The
wire is running into the page, with electron flow current shown by the arrow.
·
Oersted
wondered if the wire would be attracted towards one of the poles of the magnet…
this would mean that it would go left or right.
·
Instead,
he measured a force that (in the diagram above) pushed the wire up!
o
In
this case the force, the current, and the magnetic field are all acting at
right angles to each other.
Force à Up
Current à into page
Magnetic field
à to the right (north to south!)

·
The
three vectors are perpendicular to each other.
·
Anytime
we need to draw vectors pointing into the page (away from you) or out of the
page (towards you) we will use the following symbols…

1.
The
“into page” is supposed to look like the feathers on the end of an arrow or
dart that is flying away from you.
2.
The
“out of page” is supposed to look like the tip of an arrow coming at you.
3.
This
leads to our third hand rule.
Third
Left Hand Rule
1.
Stretch
out your fingers. Your fingers point in the direction of the magnetic field
(towards the south end of a magnet).
2.
Point
your thumb so that it is 90° to your fingers. It points in the
direction of the electron flow current in the wire.
3.
Imagine
the wire is sitting against the palm
of your hand. You could push it, correct. And that’s the direction of the force
the magnet exerts on the wire.
Look at the diagram on page 688.
·
The
only difference is that they are doing a right hand rule because
they’re doing conventional current.
Example: A current is running from left to
right in a wire across your computer screen. If the computer screen generates a
magnetic field pointing out at you, which way is the force acting on the wire?
We’ll do this in steps…
1.
We will
assume that the current is electron flow, so I’ll use my left hand.
2.
Since
the current is moving to the right, I’ll point my thumb to the right.
3.
The
magnetic field points out of the screen towards me, so I’ll point my fingers
towards myself… this might take a bit of twisting of your hand but you can do
it.
4.
You
should find now that your palm is facing up… this is where the wire is sitting,
and you’re pushing it up!
Example: Using the following diagram, tell
me which direction the current is flowing in the wire…
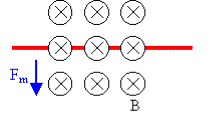
Again, we’ll solve it in steps…
1.
I’ll
use my left hand, assuming that I want to know the direction of the electron
flow current.
2.
The magnetic
field is pointing into the page (that’s what the little Ä represent), so my fingers point into
the page.
3.
The force is pointing down, so my palm has to point down, just like I was pushing
down on the wire.
4.
When I
look at which way my extended thumb
points, it’s to the right. The electron flow current is flowing in the wire to
the right!
It has been found that the magnitude of the force exerted on the wire by
the magnetic field (Fm) is directly
proportional to:
1.
The
current in the wire (I) measured in amps.
2.
The
length of wire in the magnetic field (l)
measured in metres.
3.
The
strength of the magnetic field produced by the magnet (B) measured in Teslas.
Fm = I l B
Example: How strong is the magnetic field if
2.0m of wire with a current of 10A is pushed downwards by a force of 12N?
Fm = I l B
B = Fm / Il
= 12N / (10A x 2.0m)
B = 0.60T
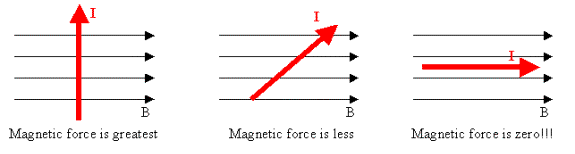
It was also quickly realized that the force also depended on the angle
the wire made with the magnetic field.
·
If the
wire is exactly perpendicular to the magnetic field, the force is at a maximum.
·
We
often say the wire “cuts through” the magnetic field.
·
If the
wire is rotated so that it is cutting through the magnetic field at an angle,
then the force decreases.
·
When
the wire is exactly parallel to the magnetic field the force is zero.
·
This
leads to an addition to the magnetic force formula given above…
Fm = I l B sinq
·
So,
when the wire is exactly perpendicular to the field (q = 90°) the force is a maximum, since
sin90° = 1.
·
If the
wire is exactly parallel (q = 0°) then the force is zero, since sin0° = 0.
·
In (almost)
all the problems in this course we will assume that the wire is exactly
perpendicular to the field, unless you are told otherwise.
You might
be thinking that with all this magnetic field stuff we’ve been calculating in
the formulas, this might be a good way to define what a magnetic field is.
·
In
fact, this is exactly how they do define magnetic field…
·
“The
magnetic field is a vector which causes a force on a current carrying wire,
placed at 90° to the field, to act at right
angles to the field and the wire.”
·
Magnetic
field is measured in Teslas (T),
although you will sometimes still see “weber per metre squared” (Wb/m2) or “gauss” (G) in some
books.
o 1 Wb/m2 = 1 T
o 1 G = 1 x 10-4 T
Common Magnetic Field Strengths
Earth’s = 5 x 10-5 T
Small Fridge Magnet = 0.01 T
Magnet in school lab = 2 T
Very strong lab magnet = 10 T
Surface of Neutron Star = 108 T