You need to be especially careful when you are doing problems involving gravity pulling something down a slope.

• The physics involved is considerably more complex than it might first seem, mostly because everything is tilted.
• Let’s look at a standard question of gravity on an inclined plane (slope) to see how we would figure it out.

Example 1:Determine the acceleration of a 15 kg box down a 30° slope if the coefficient of friction is 0.15.

The first thing we should do is sketch a free body diagram of the situation.

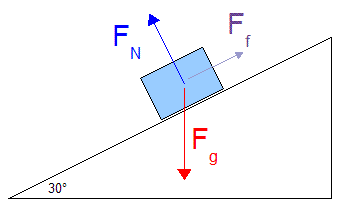Figure 1

There are a few special things you have to notice about this diagram:

• Force due to Gravity: F_g is pointing straight down, even though we are on a slope. Nothing will ever change gravity from pointing straight down. The only reason for this box to move down the slope will be a component of gravity's force.
• Normal Force: Remember that a normal force F_N is always perpendicular to the surface that you are on. Since this surface is slanted at a bit of an angle, the normal force will also point at a bit of an angle. In these questions F_g ≠ F_N
• Force due to Friction: F_f will always be opposite to the direction that something is moving. In this situation the object is moving down the slope, so friction points back up the slope.
• There is no applied force, since this would mean that there was something other than gravity actually trying to shove it down the slope.

We can calculate the force due to gravity...

F_g = mg = 15 (9.81) = 147.15 N
(Keep this unrounded number ready, so we can use it in calculations later.)

We need to break F_g up into components that point down parallel to the slope (F_//) and perpendicular to the slope (F_⊥).

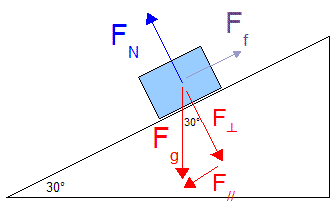Figure 2

If you are wondering how I figured out that the 30°angle is at the top of the red triangle, take a look at this...

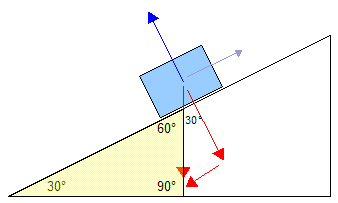Figure 3

• I created the yellow triangle by just extending the line of F_g down a bit.
• Since this makes a nice right angle triangle, I know that the angle at the top of the yellow triangle must be 60° (since the angles have to add up to 180°).
• Since F_⊥ is perpendicular to the slope, the angle in the top of the red triangle must be 30° so that they will add up to 90°.

Since we know F_g and an angle on the triangle, we can use basic trig to calculate the other two sides.

Only round off a number if it's a final answer, like if this was part (a) of a bunch of questions together. Otherwise, leave it as is so you aren't looking at the rounded off answer of a rounded off answer of a etc etc etc...

Determine F_//...

sinΘ = opp / hyp
sinΘ = F_// / F_g
F_// = sinΘ F_g
= sin30° (147.15 N)
F_// = 73.575 N
(Again, we'll keep the number unrounded. This is the force pulling it down along the slope.)

Determine F_⊥...

cosΘ = adj / hyp
cosΘ = F_⊥ / F_g 
F_⊥ = cosΘ F_g
= cos30° (147.15 N)
F_⊥ = 127.436 N
(Guess what, don't round off yet... or anything else right up to the end. Oh, and by the way, look back at Figure 2... F_⊥ is equal to the normal force, F_N!)

Determine the force due to friction using the value you just got for normal force.

F_f = μF_N
= 0.15 (127.436)
F_f = 19.115 N

Now you know the force that is taking it down the slope, and the friction that is slowing it down. Determine the net force F_NET...

I've made F_f negative because it is working against the F_//. One of them must be negative if the other is positive.

F_NET = F_// + F_f
= 73.575 + -19.115
F_NET = 54.460 N

Now, finally we can determine the acceleration of the box...

F_NET = ma
a = F_NET / m
= 54.460 / 15
a = 3.6 m/s²

Our final answer is 3.6 m/s² , and yes, we round it off.

Notice that in each step I had you sketch or determine something.

• I bet you can see how each of those could be a part of a multistep question like (a), (b), (c), etc.
• In fact, I could have about 7 or 8 parts to this question.
• If you ever do a question like that, then yes, you must round off your final answer for each step to the correct number of sig digs.
• You should still keep the unrounded off number written at least somewhere, since you should be using unrounded off numbers for the questions that follow.
• Otherwise you would end up with a final answer that's gone through about 7 roundings off!

Re-read through this example a few times. It's long and confusing at some parts, but try to look at each individual tiny calculation. Taken in little bits each part isn't as hard.