If you need to calculate the centripetal acceleration of an object but you don’t know the velocity, you would have a little bit of a problem.
- There should be a way to come up with a basic formula that relates velocity in a circle to some of the other concepts we have studied so far.
- Let’s try starting off with a formula that we know from the beginning of the course.
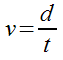
- Since we are looking at something going around in a circle, the distance it covers each revolution is equal to the circumference of the circle.
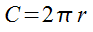
- We will substitute this into the first formula where the distance the object travels (d) equals the circumference (C) …
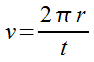
The word period is also used in other sciences, such as the "Periodic Table of the Elements" in chemistry. It is named this way because periodically the elements repeat the same characteristics.
- The last thing we need to change is the time "t" on the bottom.
- In physics, we call the time that it takes for anything to complete one full cycle or revolution the period, which has the symbol "T".
- For an object moving in a circle, the period is the amount of time needed for the object to go around exactly once.
- This gives us a slightly different looking formula.
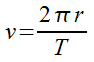
v = velocity (m/s)
π = pi, use 3.14 in your calculations
r = radius of the circle (m)
T = period (s)
Example 1: What is the length of a student’s arm if she can swing a pail in a circle at 2.72m/s every 1.5s?
v = 2πr / T
r = (vT) / (2π)
= (2.72 x 1.5) / (2π)
r = 0.65 m
You could also combine this velocity formula with the acceleration formula that we have already looked at…
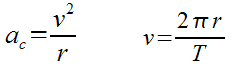
Original Formulas
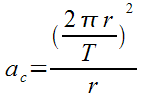
Step 1
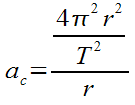
Step 2
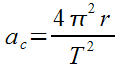
Final Formula
- This final formula does not appear on your data sheet, but you might find it useful to do some problems.
- You should be able to show how you got this formula, so don’t just blindly memorize it.
Example 2: What is the acceleration of a horse running around a circular race track with a radius of 37m once every 12s?
ac= 4π2r / T2
= 4π2(37) / 12 2
ac= 10 m/s2