The study of projectile motion brings together a lot of what you have learned in the past few chapters.

• You need to know about gravity, forces, velocity, acceleration, and vector components to be able to fully understand (and figure out) these questions.
• Don’t worry, though. Even with all that stuff to keep track of, learning how to do these questions and understand what is happening a little bit at a time makes it all manageable.

The Wile E. Coyote Effect

I’m sure all of you have seen the cartoon where the Coyote is chasing after the Road Runner and runs off of the cliff. He hangs in mid air for a second, looks down, and then starts to fall.

• The question is how true is this, and how many people believe it is true?

A few years ago some researchers in the U.S. went to elementary schools, junior and senior high schools, and universities and asked them to look at the following:

"Ignoring air resistance, which of the following correctly shows
what an object would do if it rolled off a cliff?"

Figure 1

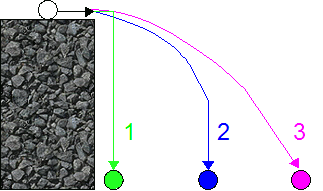
The breakdown of answers they got was almost exactly the same at all ages.

• About 60% said number 1 was correct. The object will stop in midair, and then start to fall straight down. Because this is what the Coyote always did in cartoons (and because some people actually referred to it in their explanation of why they chose this answer), the researchers called it the Wile E. Coyote Effect.
• About 25% said number 2 was correct. The object will move forward at first, but will eventually just fall straight down.
• Only about 15% answered number 3. The object will continue to move forwards the entire time it is falling.

The correct answer is actually number 3, and if you think about it using the physics you've studied it makes sense.

• Let's say a coyote does run off a cliff. As he leaves the cliff he has a horizontal velocity.
• From studying forces and acceleration you already know that the only way to change that horizontal velocity (cause an horizontal acceleration) is to exert an horizontal force on the coyote.
• If we are ignoring air resistance (which is a very good idea since it will be practically zero), then there is no horizontal force to cause an horizontal acceleration.
• Since there is no horizontal acceleration, the coyote will travel horizontally at the same speed the whole time!

That doesn't tell us anything about what is happening vertically , which is completely separate from what the object is doing horizontally.

• As soon as the coyote leaves the cliff he will experience a vertical force due to gravity.
• This force will cause him to start to accelerate in the vertical direction.
• As he falls he will be going faster and faster in the vertical direction.

Looking at this problem as what is happening horizontally and vertically, you should get the idea that this is just like the components that we were just working on a couple of lessons back.

• The horizontal and vertical components of the motion of an object going off a cliff are separate from each other, and can not affect each other.
• In a lot of books you will see the horizontal component called x and the vertical component called y.

If we look at the horizontal and vertical components of an objects velocity as it rolls off a cliff, we would get something that looks like this.

Figure 2

• The x-component is there from the start, and stays the same the entire time.
• The y-component doesn’t even exist at the beginning, but grows bigger as the object falls.
• The shape of the path that it follows is actually a parabola . If you’ve studied those in math class, great! Don't worry about it if you haven't, just as long as you recognize the shape and know the name.

To understand how to actually figure out questions involving these situations, it’s probably best to look at an example.

• Keep in mind the characteristics of the object as it falls while you go through the example.
• When you are doing a part of a question that has to do with vertical movement “THINK VERTICAL” and only use vertical ideas (like gravity).
• When you are doing a part of a question that has to do with horizontal movement “THINK HORIZONTAL” and only use horizontal ideas (no gravity/acceleration).

Example 1: I throw a ball off the edge of a 15.0m tall cliff. I threw it horizontally at 8.0m/s.

1. Determine how much time it takes to fall.
2. Determine how far from the base of the cliff it hits the ground.
3. Determine how fast it is moving vertically when it hits the ground.
4. Determine what its total velocity is when it hits the ground.

a) THINK VERTICAL

We’re talking about something falling, and that is vertical motion, so we will only use vertical ideas and numbers. It actually would take the exact same amount of time for the object to hit the ground if I just dropped it straight down from the edge of the cliff , so let’s just calculate the time to fall that way. Remember to think vertically…

d = v_it + 1/2 at² <- Initial vertical velocity is zero so...
d = 1/2 at²
t = sqr root (2d/a) = sqr root (2 x 15.0 / 9.81)
t = 1.75 s

b) THINK HORIZONTAL

Well, we know it was in the air for 1.75s (from the previous question), and it was moving at a constant speed of 8.0m/s in the x-direction the whole time, so…

v = d/t
d = v t = (8.0m/s)(1.75s)
d = 14m

It will move 14m horizontally, so it hits the ground 14m away from the base of the cliff.

c) THINK VERTICAL

It has been accelerating down the whole time. We know that gravity is causing this acceleration, and that it wasn’t moving vertically at the start, so we can figure out how fast it is going (vertically) when it hits the ground.

v_f² = v_i² + 2ad
v_f = sqr root (v_i² + 2ad) = sqr root (0 + 2 x 9.81 x 15.0)
v_f = 17 m/s

d) Combination!

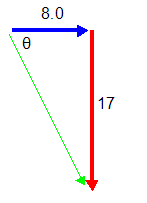
Figure 3

It’s total velocity is found by adding the horizontal and final vertical components of the velocity to find the resultant.

c² = a² + b²
= (8.0m/s)² + (17m/s)²
c = 19m/s

tanΘ = opp/adj
= (8.0m/s) / (17m/s)
Θ = 25°

The object is moving at 19m/s at an angle of 25° below the horizontal when it hits the ground.

Although there will always be slight differences in actual problems, this is the standard sort of questions that you will be asked for these types of questions.

Still having trouble with horizontal projectile motion? Then click here. Requires Windows Media Player 9 or later and a broadband connection (dial-up connection not recommended).