By now you should be saying to yourself that if an object going in a circle is accelerating, there must be a force acting on it.
- This agrees with Newton’s Laws that a force results in acceleration.
- If there were no forces involved, the object should be moving at a constant speed in a straight line, which it isn’t.
- We should be able to come up with some formulas for forces that relate directly to circular motion.
If you have already calculated the centripetal acceleration of an object moving in a circle from one of the formulas we have studied so far, then just go ahead and use F = ma to calculate the force.
- Because this is a force causing an object to move in a circle, we refer to the force as a centripetal force.
- This is written in formulas as Fc
- A lot of the time you won’t calculate the acceleration first, so we should have a couple of formulas to be able to calculate the centripetal force based on the information you do have.
Basic Formula
We’ll start with the basic force formula, and add in the centripetal acceleration formula we have from Lesson 28.
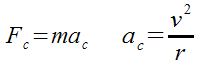
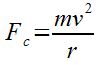
Example 1: You might have seen movies with an astronaut in training spinning around and around in this big machine to get ready for their flight. The device is called a centrifuge, like the one pictured at right (click on it to go to the Nasa website for the Center for Gravitational Biology Research). Let’s look at the forces on a 100 kg person’s body, and try to relate it back to regular Earth gravity (one “gee” = 9.81m/s2). Keep in mind that just standing on the ground the person in this example would normally weigh (Fg = mg) 9.81e2N. What is the centripetal force acting on this 100kg person if he is spun around in a 8.80m circle at…
a) 10.0m/s?
Fc = mv2 / r
= (100)(10.0)2 / 8.80
Fc = 1.14e3 NThis is the “weight” that the person will feel themselves weighing. Remember from the section on mass and weight that weight is based on how much gravity is in the area that you are in. Sticking this person into the centrifuge we are able to make them feel heavier than they really are. How much “gravity” is his body feeling?
Fg = mg -> g = Fg / m = (1.14e3 N) / (100kg) = 11.4 m/s2
This is just a bit more than regular gravity. We would say that he is experiencing 1.16 g's of gravity. We figure this out by taking the acceleration due to gravity we just calculated (11.4m/s2) and divide it by regular gravity (9.81m/s2).
b) 15.0m/s?
Fc = mv2 / r
= (100)(15.0)2 / 8.80
Fc = 2.56e3 NWow! That’s a pretty big increase in weight for just a small increase in velocity. Keep in mind that velocity is squared in the formula, so even a small increase can make a big difference. How many gees is the person feeling now?
Fg = mg -> g = Fg / m = (2.56e3 N) / (100kg) = 25.6 m/s2
That would be 2.61g … you would definitely feel very uncomfortable by this point. This is actually getting closer to the acceleration that astronauts feel going up in the space shuttle.
Second Formula
We now have a centripetal force formula to use when we know the velocity of the object. But what if we didn’t have the velocity already? Let’s look at combining these two formulas…
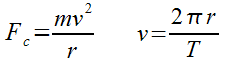
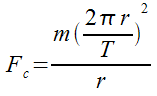
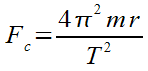
Example 2: What is the centripetal force acting on a 100 kg man in a 8.80m radius centrifuge if he is spinning at 15 rpm?
- “rpm” stands for "revolutions per minute", so we will be able to figure out a period from that.
- If he completes 15 revolutions every minute, that means he makes 15 revolutions every 60 seconds.
- To find out how many seconds it takes for one revolution (the period) we take 15 rev per 60s and inverse it!
T = 60s / 15 rev = 4.0 s per revolution
Fc = 4π2mr / T2
= 4π2 (100)(8.80) / 4.02
Fc = 2.2e3 N
