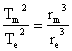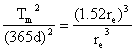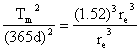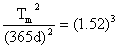Kepler took the data that Brahe had spent his life collecting and used it (especially the information on Mars) to create three laws that apply to any object that is orbiting something else.
- Although Kepler’s math was essentially wrong, the three laws he came up with were correct!
- It would be like you writing a test, and even though you did all the work on a question wrong, you somehow get the correct final answer.
- Kepler’s Three Laws of Planetary Motion are still the basis for work done in the field of astronomy to this day.
Kepler’s First Law
Kepler’s First Law went against the major assumption that scientists of the time had about orbits… in fact it is probably against the image of orbits that you have!
- If I asked you to describe or draw a sketch of the Earth’s orbit around the sun, how would you draw it. Think about in your head.
- You’d probably stick the sun in the centre and draw a circle around it to show the path the Earth takes.
- In fact, this is totally wrong, as Kepler’s First Law states…
“The path of any object in an orbit follows the shape of an ellipse,
with the orbited body at one of the foci.”
So what does all that mean?
- An ellipse is shaped like a circle that someone has sat on. It’s squished in the middle and bulges out on the ends.
- Foci (the plural form of the word focus) are two points inside the ellipse.
- If you were to push stick pins into the foci and put a loop of string around them, you could draw an ellipse.
- This means we have a shape that looks like this…

Remember that the object being orbited sits at one focus, and the other object follows the path of the ellipse.
- The sketch of the Earth orbiting the Sun should look like this…

- This means that sometimes the Earth is closer to the Sun, and sometimes further away.
- This is not the reason for summer and winter!
- The seasons on Earth are created by Earth’s tilt on its axis.
The diagrams I have drawn here are exaggerated quite a bit to show the elliptical shape and focus clearly.
- The true orbit of planets isn’t this much flattened out.
- This elliptical shape does not apply to just planets orbiting the sun. It works for any object orbiting any other object.
- If you measured the orbit of the Moon around the Earth, it would have an elliptical shape, and so would any satellite in orbit around the Earth.
- Since orbits around the Earth are quite small, their shapes are almost a circle.
Newton was able to show that his laws of gravitation gave the same results as Kepler's. In fact, Newton was able to take things farther with his strong math background to show that the shape of the orbits were conic sections (for those of you that have seen that stuff in math). We'll be looking more at Newton's contributions in a lesson coming up.
Kepler’s Second Law
Kepler’s Second Law is based on the speed of the object as it orbits.
- In the Earth-Sun example shown in Figure 2, the Earth will travel faster and faster as it gets closer to the sun.
- As the Earth moves away from the sun, it will move slower and slower.
- It’s almost like the Earth is being “slingshot” around the sun very quickly as it passes near it.
Kepler didn’t talk about speed when he wrote out his second law. Instead, he looked at a mathematical detail that pops out because we are talking about ellipses.
“An imaginary line from the sun to the planet
sweeps out equal areas in equal times.”
If we were to look at the area the Earth sweeps out in a 15 day period, first when close to the sun (Figure 3) and then when far away (Figure 4 ), we would get diagrams that look like this.


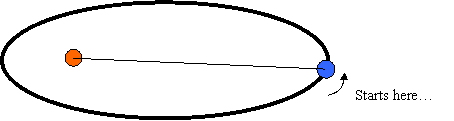
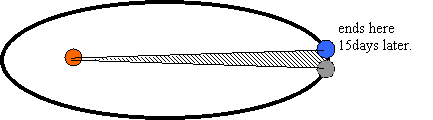
Notice how in Figure 3 we have a stubby, fat, (basically) triangular area that was swept out by the line, but in Figure 4 we have a tall, thin, (basically) triangular area swept out.
- If we calculate the area that I have (more or less) shaded in as triangles, you would find that they are equal.
- This just shows that the planet is moving a lot faster when it is closer to the sun, since you can see that it traveled a greater distance along its orbit during that time.
Kepler’s Third Law
The big mathematical accomplishment for Kepler is in his Third Law, where he relates the radius of an orbit to it’s period of orbit (the time it takes to complete one orbit).
- Now, here's the weird part. Students in Alberta need to know about this law, be able to basically explain it, but are not required to do actual calculations with it.
- After the definition is explained, and the formula has been shown so you can recognize it, you can stop. Just stop where I put "the sign" if you want to. The rest of the notes are purely for the interest of people that want to know how this formula works.
“The square of the period of orbit,
divided by the cube of the radius of the orbit,
is equal to a constant (Kepler’s Constant) for that one object being orbited.”
The formula looks like this...
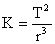
T = period (in any unit)
r = radius (in any unit)
K = Kepler's Constant
There's a few weird things about this formula compared to many other physics formulas:
- You can measure the period and radius in any units you want, as long as you keep them consistent for the whole question.
- The radius is the average radius of the orbit. When Kepler did his original calculations he assumed a circular orbit in these calculations, even though this went against his own First Law.
- Kepler's Constant is only a constant if the object being orbited stays the same. So, anything orbiting the sun has the same Kepler's Constant, just like anything orbiting the Earth has the same Kepler's Constant. The Sun and Earth Kepler's Constants will be different from each other.

- You can see for these values for a three different planets all orbiting the Sun I get (within experimental error of course) the same value for Kepler's Constant.

Example 1: Using the values for Kepler’s Constant that were calculated above for Earth, Mars, and Jupiter orbiting the sun…
a) determine the average Kepler’s Constant for anything orbiting our sun.
b) Neptune has an average orbit of 4.5e12 m from the sun. Determine how long it takes to complete one orbit.
a) The average of the three values is 3.99e-29.
b) T2 = Kr3 = (3.99e-29) (4.5e12m)3 = 6.0e4 days = 165 years!
It takes Neptune about 165 years to go once around the sun!!!
You can also write out this formula a couple of other different ways. They are just ways of rearranging things.
- We know that Kepler’s constant will be the same for any objects orbiting the same thing.
- It would be like doing one set of calculations for Earth and another for Mars like we did in the table above. The K values are the same, so we can just stick their formulas together.
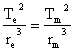
e -> values for Earth
m -> values for Mars
- This formula is usually re-written to look like this…
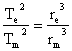
- You don’t have to have “e” and “m” in the formula. I just used those because we were talking about Earth and Mars in the last example.
- You could just as easily use “a” and “b”, just as long as you put both the “a” on top, and both the “b” on the bottom.
- You can also use this version of the formula to do tricks if you are missing some information, as the next example shows.
Example 2: If the orbit of Mars is 1.52 times greater than the orbit of Earth, determine how much time it takes Mars to complete one orbit.
If I was able to look up the orbit of Earth in a book, this would be a fast question. All I would do is multiply that number by 1.52 to get the orbit of Mars, and then I would have both the radii I need. But what if I was doing this question on an exam and I didn’t know the value for Earth’s orbit.
Note: Do not use the “Radius of Earth” number on your data sheet. That is the distance from the centre of the Earth to the surface of the Earth, not the size of Earth’s orbit.
Here’s what I do know…
rm = 1.52 re
Te = 365 days
Let’s see if we can substitute that into the formula…
Tm = 684 days