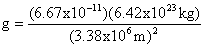Remember a few weeks ago we were talking about Sir Isaac Newton and his goal to figure out gravity… the whole “apple” thing.

• It seems like we got sidetracked a bit, since we talked about his three laws (Lessons 15, 16, 17), but those really have (apparently) little to do with gravity.
• About all we did do is write the formula F_g = mg , but that doesn’t explain gravity.
• Newton actually did try to explain gravity itself, and was partially successful, with his Law of Universal Gravitation.

Newton started with the idea that since the Earth is pulling on the apple, the apple must also be pulling on the Earth (Newton’s 3rd Law).

• Ask a person on the street where gravity comes from in this situation, and they'd probably say "the Earth". They would never consider the apple as a "source" of gravity.
• But if the apple is pulling on the Earth, that must mean that an object doesn’t have to be huge to have a gravitational pull on other objects. There is nothing special about the Earth compared to the apple... both are sources of gravity.
• That would mean that one apple should be able to have a gravitational pull on another apple… that means any mass pulls on any other mass.
• The reason we don’t see the effect of, for example, you being pulled towards your computer mouse, is that the masses are so small that the force is also very small.
• Still, the force is there, and Newton wanted to come up with a way of calculating it.

Using a lot of calculus and some pretty tough physics he came up with this formula:

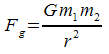
F_g = force due to gravity between the two objects (N)

G = the Gravitational Constant

m₁ and m₂ = the two masses (kg)

r = the distance between the two objects’ centres (m)

This formula shows that any objects with mass will pull towards each other with a gravitational force.

• We usually say that an object has a gravitational field around it.
• Any field is just a sphere of influence around the object. The closer you get, the more you are affected by it.
• In the case of gravity, the bigger the mass of the object, the bigger the field.
• The formula also shows that the closer the objects are, the greater the effect of the gravitational field.

Newton then turned his attention to trying to find the value for the Gravitational Constant, “G”.

• Nope, it isn’t the acceleration due to gravity on Earth, 9.81m/s².
• Newton looked for a way of calculating the value for G from the formula above. If we solve that formula for G we get:

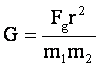
Let’s look at how we will substitute numbers into this formula.

• Newton realized that the only thing he could measure a F_g for would be an object on Earth’s surface. An example would be you. We could calculate the force due to gravity on your body easily using F_g = mg.
• We need to know the distance from the centre of the Earth to your centre… which we do have: 6.38e6 m. And yup, they even had a pretty good estimate of this in Newton's time!
• We need to know your mass, which would be m₁… that’s no problem.
• The last thing we need, m₂, is the mass of the Earth. Oh, oh. That one is a problem.
  • In Newton’s time no one had any idea how heavy the Earth really was.
  • If we knew G, then we could calculate the mass of the Earth, but that’s what we are trying to calculate here!
• Newton continued to look for some way to calculate G indirectly, but never found a way.

Henry Cavendish

About a 100 years later a man named Henry Cavendish finally figured out a way to measure the value for G.

Cavendish's Torsion Balance

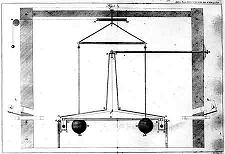
• He attached a really heavy pair of metal balls to the ends of a long metal rod, and then hung the rod from a wire.
• He then brought another pair of really heavy metal balls near the balls on the rod.
• Cavendish knew that because they had mass they should pull on each other, but very weakly.
• To measure this weak pull, he carefully measured how much the wire was twisting (torque) whenever he brought the other masses near by.
• This is why the device he used is called a torsion balance.

After a lot of very careful, very tedious tries, he found that G was 6.67e-11Nm²/kg².

• Cavendish realized that because he knew the value for G, he could now calculate the mass of the Earth. That’s why he titled the paper that he published “Weighing the Earth.”

Example 1: Using values that you now know, determine the mass of the Earth.

We know that the force exerted on my body by the Earth is F_g = mg , where little “m” is my mass.

I also know that the force could be found using Newton's big Universal Gravitation Formula, where one mass is a little “m” (my mass), and the other mass is a big “M_e” (the mass of the Earth).

F_g = F_g

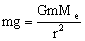
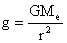
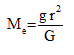
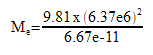
M_e= 5.99e24 kg

Notice that we were able to combine a couple of formulas to get the new formula .

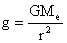
• M_e does not always have to be the mass of the Earth. It could be the mass of the moon, Mars, an asteroid, whatever!
• It let’s you calculate the acceleration due to gravity on that object if you know the other values.

Example 2: The planet Mars has a mass of 6.42e23 kg and a radius (from its centre to the surface) of 3.38e6 m. How much would a 60 kg person weigh on Mars compared to their weight on Earth? Determine How heavy he would “feel” he weighed in kilograms on Mars.

On Earth the person has a weight of…

F_g = mg

= (60kg) (9.81m/s²)

F_g = 5.9e2 N

Gravity on Mars can be found using the formula shown above. Note: On an exam you need to show how you got this formula.

g = 3.75m/s²

So that person’s weight on Mars will be…

F_g = mg

= (60kg) (3.75m/s²)

F_g = 2.3e2 N

Remember, mass never truly changes... it's a constant. This is just how much you would feel like, in measurements you can better understand.

To figure out how much he would feel like he weighed on Mars in kilograms, remember that we spend our lives here on Earth and our body thinks that 9.81m/s² is what gravity should always be. Therefore, this person will feel like his mass is…

F_g = mg

m = F_g / g

= (2.3e2 N) / (9.81m/s²)

m = 23 kg

Example 3: Determine the force of attraction between a 15.0kg box and a 63.0 kg person if they are 3.45m apart.

I have to assume that the distance I have been given is the distance between the two centres of the objects.

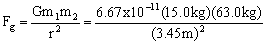
F_g = = 5.30e-9 N

In the end, Newton still hasn’t really explained why there is gravity, or how it actually works, but he did create a formula that shows how gravity can be calculated as a force between pairs of objects.

• You need to jump ahead to the 1900’s (and even present day) to get even a bit of an explanation of what gravity really is.