You’ve probably heard of kinetic energy in previous courses using the definition and formula…

Any object that is moving has kinetic energy.

E_k = ½ mv²

E_k = kinetic energy (J)
m = mass (kg)
v = velocity (m/s)

We’re going to keep on using that basic formula, but we do need to clear up the definition a little bit.

What is “any object”?

• “Any object” just refers to anything that we can measure as having a mass.
• This covers everything from small subatomic particles like electrons all the way up to galaxies.
• Make sure that in any calculations you have the mass measured in kilograms.

What is "moving"?

We need to ask “Moving relative to what?”

• Right now you’re sitting motionless reading these notes, so you have no kinetic energy, right?
• This is true relative to the reference frame of the room you’re in. Isn’t the earth spinning on its axis? Isn’t the whole planet moving around the sun?
• You need to make sure that you are always sure about what your measurements are being taken in relation to.
• Most of the time we measure stuff relative to the surface of the earth, so it doesn't have to get complicated. Still, be careful.
• Also be sure to only measure velocity in metres per second.

Example 1: A pop can with a mass of 312g is sitting in the cup holder of my car as I drive down Yellowhead at 68 km/h.

a) Determine how much kinetic energy it has relative to me in the car.

E_k = ½ mv²

But relative to me the pop can’s velocity is zero, so…

E_k = 0 J

b) Determine how much kinetic energy it has relative to someone standing on the side of the road.

E_k = ½ mv²

= ½ (0.312 kg) (19 m/s)²

E_k = 56 J

Be ready to manipulate this formula to solve for other variables…

Example 2: Determine the velocity of a 150 kg cart if it has 3.60e4 J of kinetic energy.

First, see if you can correctly solve the formula for “v”. This is one of the manipulations that students commonly mix up! You should get…

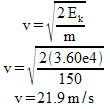
The concept of kinetic energy can also come in handy if you need to perform calculations of the work done, as the following example shows…

Example 3: I am driving my 2500 kg Camaro down the street at 52 km/h. I notice that there is a school zone ahead, so I hit the brakes to slow down to 24 km/h. If I slowed down over a distance 145 m, determine the average force applied by the brakes.

Remember to keep the complete number from your calculator written down on scrap paper… that’s the number you want to use in your calculations before rounding off at the end of the problem.

First, you’ll need to change those velocities from km/h into m/s…

v_i = 52 km/h = 14 m/s

v_f = 24 km/h = 6.7 m/s

Next, calculate the change in kinetic energy of the car as it slowed down…

• You could just do a regular calculation of the initial kinetic energy and subtract it from a regular calculation of the final kinetic energy after, or you can use a formula derived this way:

Since work is a change in energy W = Δ E_k . Work also equals force times displacement, W = Fd.

Δ E_k = W

Δ E_k = Fd

F =Δ E_k / d = (-2.1e5 J) / (145m)

F = -1.4e3 N

The negative sign just shows that the force is being exerted in the opposite direction to the velocity of the object.

The fact that work is equal to the change in energy in a situation is usually called the “Work-Energy Theorem”

• It basically just means that you can do calculations like the ones we did above and you’ll get the right answer.
• You can take this even further once you combine the ideas of kinetic energy with potential energy.