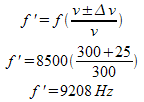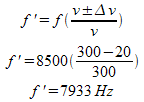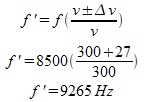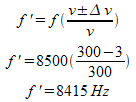You’ve probably noticed that when an ambulance passes you with its siren going you will hear the sound change.

• As it comes closer to you the pitch (frequency) of the siren will seem to increase.
• When it passes you and continues on, it seems like the frequency drops.
• Any change in the apparent frequency of a source of sound as measured by an observer as they move relative to each other is known as the Doppler Effect.

Christian Doppler described the Doppler Effect in 1842.

• In his version of the experiment, he had trumpet players stand on a flatbed train car and move past a stationary observer.
• The observer recorded the notes that he thought the trumpet players were playing.
• Doppler used the differences in the frequencies to help create a formula that could be used to calculate the changes.

Bob the Swimming Bug

To see why this change in frequency happens, I want you to imagine a very special bug named “Bob.”

• I have trained Bob to do a very special trick. He can tread water!
• When I first trained him to do this, he could only do it while staying in exactly one spot. If we were to look down on Bob as he treads water, we would see waves that look like Figure 1…

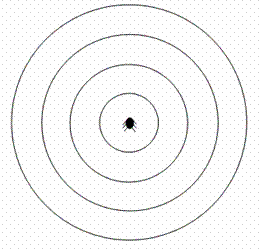
Notice how Bob is in the middle and all the waves are spreading out evenly from him in the water.

• If I asked you to stand on the right side of Bob, and then on the left of Bob, and measure the frequency of the waves (how many pass you per second) you would give the same number.
• Let’s say that Bob is bobbing up and down at exactly 4 Hz, and he always treads water at this frequency. No matter where you are standing, you will measure the same frequency for Bob's waves.

After years of training I am able to get Bob to tread water while slowly moving to the right.

• Each time he starts to make a new wave, he’ll be in a spot slightly to the right of where he used to be.
• That means the centre of each new circle will be slightly to the right of where he made his previous wave circle.
• The red circle is the first wave he made, then blue, pink, and finally black.
• Each wave ripple continues to spread out as Bob moves to the right.

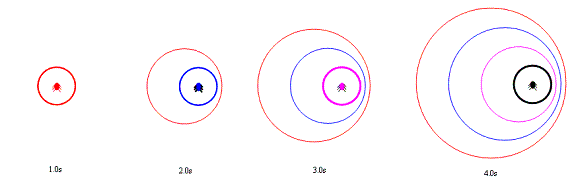
• At one second Bob is at the centre of the red wave he has created.
• At two seconds he is at the centre of the next wave he is creating, a blue one. His red wave continues to grow outwards with its centre where he was at 1.0s.
• At three seconds the pink circle is created with Bob at the centre. The blue and red circles are still expanding with their centres at the same spots as when they were originally created.
• This pattern would continue for as long as Bob is bobbing up and down and moving to the right.

Now let’s look at what you would measure about Bob’s frequency if you were standing on the left side compared to the right side. Remember that Bob is actually treading water at 4 Hz.

• On the left side the waves have been spread out more.
  • If I was standing on the left side and looking at the waves passing me, I would say they have a lower frequency, like 2Hz. They are not passing me as frequently.
• On the right hand side the waves are squished together.
  • If I was standing on the right side, I would say that the waves have a higher frequency, like 6Hz. They are passing me more frequently.
• In both cases you measured a frequency of Bob’s treading that is different from his true frequency, but you have no way of knowing this unless you have measured his true frequency when he was motionless.
• The exact same thing happens with sounds!

Imagine that instead of Bob, you now have an ambulance coming towards you with its siren going.

• If the ambulance is coming towards you will hear a higher frequency sound because the waves are squished together, just like standing on the right hand side of Bob.
• If the ambulance is moving away you will hear a lower frequency because the waves are more spread apart, just like standing on the left of Bob.
• You will get the same effect if the ambulance was sitting still and you were moving towards it (squishing the waves together), or away from it (spreading them apart).
• The Doppler effect (the apparent change between the true frequency and the measured frequency) will happen if there is any difference between the velocity of the source and the observer.

There is a formula that lets you calculate the apparent frequency of a sound if you know the true frequency of the sound and the difference in velocity between the source and the observer.

• The formula I am giving you is different from the one in the textbook, and does not appear on your data sheet. I will give the formula to you if you ever need it.

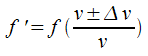
f ‘ = apparent frequency (Hz)
f = true frequency (Hz)
v = speed of sound (m/s)
Δv = difference in velocity between source and observer (m/s)

• If the observer and source are moving closer towards each other, use the plus sign.
• If the observer and source are moving further apart, use the minus sign.

Example 1: A person is running around screaming at a frequency of 8500 Hz after hitting his thumb with a hammer. It is a cold day and the speed of sound is 300m/s.

a) If he is running towards you at 25 m/s (wow, that’s fast!) what frequency will you hear his scream as?

b) If he is running away from you at 20m/s what frequency will you hear?

c) If he is running toward you at 15m/s while you run towards him at 12m/s, what frequency will you hear?

d) If he is running towards you at 17 m/s and you are running away from him at 20m/s, what frequency will you hear?

To figure these out, use the formula you were given above. Be careful with the difference in velocity between the source and the observer. I’m not going to be careful about sig digs in my calculations here because I want you to easily see how the frequency changes. You still need to use sig digs when you do your calculations!

a) The source is approaching the observer at 25m/s, so we will use the positive sign.

b) The source is moving away from the observer at 20 m/s, so we use a negative sign.

c) The source and observer are moving closer together at (15m/s + 12 m/s) 27 m/s, so use the positive sign.

d) The source and observer are moving apart at (20m/s – 17m/s) 3 m/s, so use a negative sign.