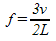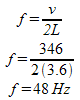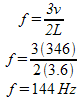Many musical instruments depend on the musician in some way moving air through the instrument.
- This includes brass and woodwind instruments, as well as instruments like pipe organs.
- All instruments like this can be divided into two categories, open ended or closed ended.
- A “pipe” can be any tube, even if it has been bent into different shapes or has holes cut into it.

An open ended instrument has both ends open to the air.
- An example would be an instrument like a trumpet. You blow in through one end and the sound comes out the other end of the pipe.
- The keys on the trumpet allow the air to move through the "pipe" in different ways so that different notes can be played.

A closed ended instrument has one end closed off, and the other end open.
- An example would be an instrument like some organ pipes (although in some designs they are open), or a flute.
- Although you blow in through the mouth piece of a flute, the opening you’re blowing into isn’t at the end of the pipe, it’s along the side of the flute. The end of the pipe is closed off near the mouth piece.
The frequencies of sounds made by these two types of instruments are different because of the different ways that air will move at a closed or open end of the pipe.
- The diagrams that I will be drawing are based on the way the air will move as a wave.
- Although the sound waves actually travel through the pipes as longitudinal waves, I will be drawing transverse waves. This is just because they are easier to draw and recognize in the diagrams.
Identifying Fractions of Wavelengths
Before we look at the diagrams of the pipes, let’s make sure that you know what fractions of a wave look like. This will be important in the way you interpret the diagrams later.
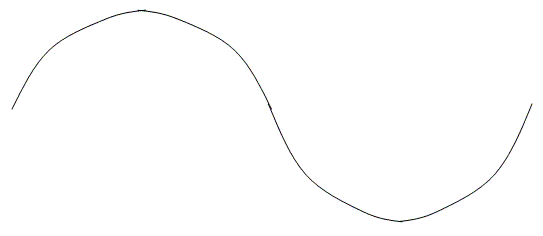


These wave fractions might appear upside down, flipped over, turned around, etc., but they will still represent portions of a wave.
- When we are talking about the sounds that pipes can make, what we are really concerned with is how much of the wave we can fit into the pipe.
- Different amounts of a wavelength in a pipe will result in a different frequency being heard.
- Because these are the frequencies of the waves that will naturally resonate in the pipes, we call them the resonant frequencies.
- In music, you might have heard these referred to as harmonics.
Although the actual length of the pipe remains the same, different notes are played.
- If you have ever played a wind instrument, you know that with the same keys pressed you can play different notes by controlling how you blow into the instrument… the difference between let’s say a low C and a high C note.
- The lowest note you can play (which is also the smallest part of the wave that can fit inside the pipe) is usually called the fundamental.
- Fitting in more of the wave produces different notes, different harmonics.
Closed Ended Pipes

Remember that it is actually air that is doing the vibrating as a wave here.
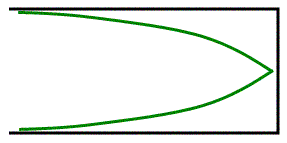
- The air at the closed end of the pipe must be a node (not moving), since the air is not free to move there and must be able to be reflected back.
- There must also be an antinode where the opening is, since that is where there is maximum movement of the air.
- The simplest, smallest wave that I can possibly fit in a closed end pipe is shown in Figure 5.
- Notice how even though it has been flipped left-to-right and it looks squished and stretched a bit to fit, this is still ¼ of a wavelength.
- Since this is the smallest stable piece of a wave I can fit in this pipe, this is the Fundamental, or 1st Harmonic.
Since the length of the tube is the same as the length of the ¼ wavelength I know that the length of this tube is ¼ of a wavelength… this leads to our first formula:
L = ¼ λ
- “L” is the length of the tube in metres. On it’s own this formula really doesn’t help us much.
- Instead, we have to solve this formula for λ and then combine it with the formula v=fλ to get a more useful formula:
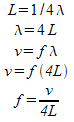
f = frequency of sound (Hz)
v = velocity of sound in air (m/s)
L = length of tube (m)
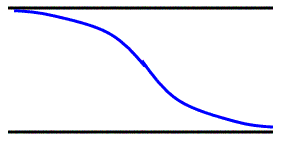
When the wave reaches the closed end it’s going to be reflected as an inverted wave (going from air to whatever the pipe is made of is a pretty big change so this is what we would expect. It would look like Figure 6.
- This does not change the length of the wave in our formula, since we are only seeing the reflection of the wave that already exists in the pipe.
What does the next harmonic look like? It’s the 3rd Harmonic.
- I know this name might seem a little confusing (I’m the first to agree with you!) but because of the actual notes produced and the way the waves fit in, musicians refer to the next step up in a closed end pipe instrument as the 3rd harmonic… there is no such thing as a 2nd harmonic for closed end pipes.
- In fact, all of the harmonics in closed end pipes are going to be odd numbers.
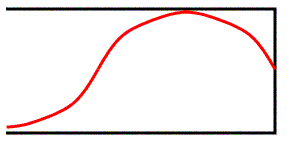
Remember that we have to have an antinode at the opening (where the air is moving) and a node at the closed end (where the air can’t move). That means for the 3rd harmonic we get something like Figure 7.
This is ¾ of a wavelength fit into the tube, so the length of the tube is…
L = ¾ λ
- This is the third harmonic of the closed end pipe. The formula for the frequency of the note we will hear is…
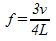
- Do you notice a pattern forming in the formulas? Hopefully, because for both open and closed end pipes, we will only give you the formulas for the fundamentals lengths. You need to remember how to get the rest.
If we drew in the reflection of the third harmonic it would look like Figure 8.
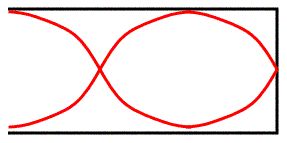
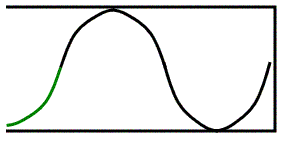
One more to make sure you see the pattern. The 5th Harmonic (Figure 9).
- There is one full wavelength in there (4/4) plus an extra ¼ of a wavelength for a total of 5/4. The length of the pipe is…
L = 5/4 λ
And the note produced by the 5th Harmonic is found using the formula…
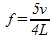
Figure 10 shows the reflection of a 5th Harmonic for a closed end pipe.
Open End Pipes
I know you’re probably thinking that there couldn’t possibly be any more stuff to learn about this, but we still have to do open end pipes. Thankfully, they’re not that hard, and if you got the basics for closed pipes it should go pretty fast for you.
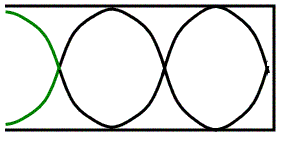
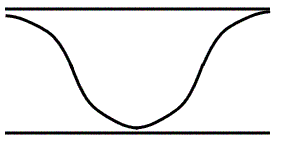
- The fundamental (first harmonic) for an open end pipe needs to be an antinode at both ends, since the air can move at both ends.
- That’s why the smallest wave we can fit in is shown in Figure 11.
- This looks different than the ½ wavelength that I showed you in Figure 3, but it is still half of a full wavelength.
- That means the length of the tube and frequency formula are…
L = ½ λ
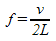
- The whole thing after it reflects at the other end looks like Figure 12.
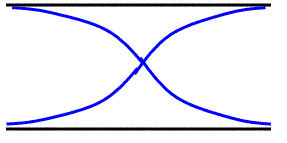
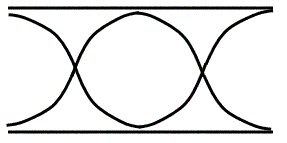
The next note we can play is the 2nd harmonic.
- Yep, open end pipes have a 2nd harmonic… they can have any number harmonic they want, odd or even.
- Again, it kind of looks weird, but trace it out and you’ll see that there is exactly one wavelength here.
- The length and frequency formulas are…
L = 2/2 λ
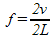
I’m not going to show you what the 3rd harmonic looks like. Instead, try drawing it yourself and see what you get.
- As a hint to help you, the formulas for the length and frequency are…
L = 3/2 λ
Example 1: An open ended organ pipe is 3.6m long.
a) What is the wavelength of the fundamental played by this pipe?
b) What is the frequency of this note if the speed of sound is 346m/s? (Calculate it using the formulas you’ve just learned, although if you wanted you could use v = f λ)
c) What note could be played as the third harmonic on that pipe?
d) If we made the pipe longer, what would happen to the fundamental note… would it be higher or lower frequency?
a)
L = ½ λ
λ = 2L
λ = 2(3.6m)
λ = 7.2 mb)
c) Notice that the third harmonic is three times bigger than the first harmonic.
d) If we made the pipe longer, the wavelength would be bigger (just look at the formula in part "a" of this example), and since wavelength and frequency are inversely related, that means the frequency would be smaller.