Back in Lesson 48 we briefly discussed refraction.
- You should remember the definition that it is the bending of light as it travels from one medium to another.
- What we will be looking at here is an actual formula that lets you calculate how much the light is bent.
- We will also look at how refraction is just one thing that happens to the light as it passes from one medium to another.
Changes in Angle
If someone is standing in a swimming pool, the light traveling through the water from the person’s feet must be bending and moving in another direction when it enters the air.
- Your brain will assume that the light was traveling in a straight line which makes their feet appear to be in a different spot, making the person look shorter.
- Since Ptolemy’s time (about 100AD) people knew about refraction, but they didn’t know why it happened, or how to predict and calculate it.
In the year 1600 a Dutch mathematician named Willebrord Snell was playing around with numbers and figured out a formula that fit what everyone was measuring.
- The Law of Refraction (AKA "Snell’s Law") in its basic form allows us to do calculations of how a beam will bend when it moves from one medium to another. In its full form, it also lets you do calculations involving wavelength and velocity of light in different media.
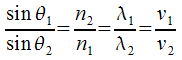
θ = angle measured from normal
n = index of refraction for medium
λ = wavelength of light
v = velocity of light
The index of refraction (n) is a way of comparing the “optical density” of different materials.
- Think of optical density as a measurement of how easily light can travel through the material.
- A low index of refraction (like water nw = 1.33) is pretty easy to travel through.
- A high index (like diamond nd = 2.42) is difficult for light to travel through.
- The index of a material is usually measured in an actual experiment… there’s no reliable way to just predict what they will be.
- Index of refraction has no units and is based on how light travels in a vacuum.
| Medium | Index |
|---|---|
| Vacuum | 1.00 |
| Air* | 1.0003 |
| Water | 1.33 |
| Ethanol | 1.36 |
| Glycerin | 1.47 |
| Crown Glass** | 1.50-1.62 |
| Quartz | 1.54 |
| Flint Glass** | 1.45-2.00 |
| Diamond | 2.42 |
* Simply use 1.00 in calculations
** Varies slightly due to inconsistencies in the glass
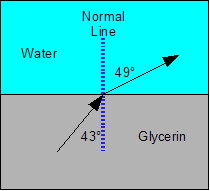
Example 1: A beam of light traveling in glycerin hits the boundary between itself and water at an angle of 43° from the normal. Determine the angle of refraction through the water.
Just like in the examples we did earlier in the waves section, we can call the original beam traveling in the glycerin the incident ray, and the light traveling in the water the refracted ray.
We can look up the indices for glycerin and water from the table above and figure out the angle… we can call either of them “one” and the other “two” as long as we stay consistent.
I’m going to say water is one and glycerin is two, and that way I don't have to do as much cross multiplying.
We only use the terms in Snell's Law that we need, and drop the others.
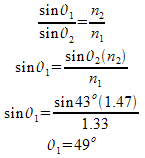
Make sure your calculator is in degree mode for these calculations!!!
As you can see from the example above, you don’t use all of the formula at once in a question.
- You only ever use two terms in any one question.
- We will usually give you three pieces of information and then you have to solve for the fourth.
We will usually be describing refraction in terms of whether the beam of light bends away from or closer to the normal.
- Going from more dense to less dense = bend away
- Going from less dense to more dense = bend towards
Using Snell's Law to Predict Changes in Wavelength
You don’t usually see color changes for regular light, since regular white light has all of the colors of the rainbow and a shift in wavelength doesn’t change anything overall.
- Using a pure colour (like from a laser) can result in a noticeable color shift.
- We will only use the part of the formula that has wavelengths and indices.
Example 2: A beam of red light (λ = 700nm) is traveling through water (n = 1.33). If it leaves the water and travels into a piece of flint glass (n = 1.75), determine the color (approximately) that it will be.
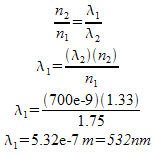
This makes it a greenish color, maybe a little on the yellowish–green side.
Speed of Light
Notice in the formula that the velocity of light will change in different media.
- The speed of light is a constant in one particular medium.
- Switch to a different medium and the speed of light will be a different constant in that medium.
- The speed that we use (3.00e8m/s) is the speed of light in a vacuum.
Scientists have successfully slowed light down to about 1 km/h! Although this is tough to do, it is possible.
- It is even possible for light to go faster if it is in a medium with an index of refraction less than 1.0.
- This does not break Einstein’s rules about the speed of light being the fastest speed.
- He said no thing (with mass) can go faster than 3.00e8m/s… light doesn’t have mass!
- And, in a particular medium, the speed of light is still the fastest possible speed.
Using the speed of light is actually one of the best ways to measure the index of refraction for an unknown material.
- Have light traveling initially through a vacuum enter the substance and measure its speed. From that you can calculate the index of refraction.
Example 3: A student is doing a lab. They test a material that light travels at 2.21e8m/s through. Determine what substance this might be.
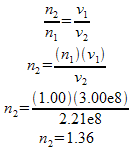
From the chart we have a substance with an index of refraction of 1.36 could be ethanol. There might be other substances with this same index, so we can’t be sure.