To do questions involving objects launched from the ground upwards at an angle (like kicking a football up into the air and watching it as it arcs in the air and comes back down), you need to add a few more steps to the way you did the questions for objects launched horizontally in Lesson 26.
- There are actually two ways to do these types of problems, one based on the vertical velocity of the object, the other based on the vertical displacement.
- The only big difference in these methods is how we are going to calculate the time that the object spends in the air.
- Choose whichever method you are most comfortable with, and whichever one suits the particular question you are doing.
- We will look at each and then it’s up to you to figure out which way you will approach a problem.
- Please be aware that some questions can only be figured out one way or the other, but not both ways.
Vertical Velocity Method
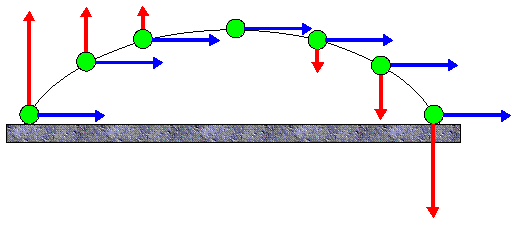
Imagine for a moment that you are watching an object as it rises into the air after you kick it upwards at an angle. Look at Figure 1 below as you read through this description.
- When it left your foot, it was going at the fastest that it can possibly move during its flight.
- The instant it leaves your foot, gravity is pulling down on it, causing it to have less and less vertical velocity.
- Remember that there will be no change in the horizontal component of its velocity.
- When it reaches the highest point in its flight, it isn’t moving up, and it isn’t moving down, for an instant of time… its vertical velocity is ZERO!
- By the time it reaches the ground again, it will still be moving with its original horizontal velocity and will have just as much vertical velocity as when it left your foot. It will have the exact same velocity as it left your foot with!
We can use this information about its vertical movement to make some calculations. We know...
- that there is gravity (-9.81m/s2) causing the acceleration on the object vertically.
- the initial vertical velocity of the object.
- the final vertical velocity of the object. We can even use this two ways, since we can say that the final vertical velocity happens at the halfway point (zero m/s), or when it gets back to the ground (same as it left the ground at).
This gives us enough information to calculate the maximum height of the flight, and the time it spends in the air. After that, we can calculate just about anything…
Example 1: You kick a soccer ball at an angle of 40° above the ground with a velocity of 20m/s.
- How high will it go?
- How much time does it spend in the air?
- How far away from you will it hit the ground (aka range)?
- What is the ball’s velocity when it hits the ground?
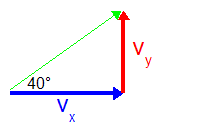
Before we can calculate anything else, we first need to break the original velocity into components.
We do this so we have a vertical component to do the first couple calculations with. The horizontal component will be used later.
Figure 2sinΘ = opp/hyp
opp = sinΘ (hyp)
= sin 40° (20m/s)
opp = vy = 13m/sa) THINK VERTICAL!
At its maximum height, halways through its flight, the object won't be going up or down, so we'll say that its final velocity at that point is zero.
vf2 = vi2 + 2ad
d = (vf2 - vi2) / 2a
= (02 - 132) / 2(-9.81)
d = 8.6 mThe ball will reach a maximum height of 8.6 m.
b) THINK VERTICAL!
Same ideas as above...
a = (vf - vi) / t
t = (vf - vi) / a
= (0 - 13) / -9.81
t = 1.3 sBut this is only the time to the halfway point, so the final answer is 2.7s.
c) THINK HORIZONTAL
It is moving at a constant velocity horizontally during the whole time we just figured out, so let’s use Figure 2 that was drawn above to get the horizontal component of the velocity.
cosΘ = adj/hyp
adj = cos Θ (hyp)
= cos 40° (20m/s)
opp = vy = 15m/sv = d/t
d = vt
= 15m/s (2.7s)
d = 41 m41m is the horizontal distance (range) that it has traveled.
d) The ball’s velocity when it hits the ground is exactly the same as when it was originally launched… 20 m/s at 40° up from the horizontal. The only difference is that now it's spiking into the ground.
Vertical Displacement Method
To do the problem this way, we must assume that the object strikes the ground at exactly the same height that it was launched from. This is the case for most questions.
When you look at how the object has moved in Figure 1, you’ll notice that it has a total vertical displacement of zero.
- In the vertical direction, it started on the ground and it ended on the ground. That's all that matters!
- Since displacement is just how far you are from where you started, and right now I’m only looking at vertical motion, the displacement is zero.
Example 2: Redo part (b) of the example that we did above. The other parts should still be done the same way (basically).
b) THINK VERTICAL!
Use the vertical velocity we calculated above as necessary. The vertical displacement is zero (from start to end), so…
d = vit + 1/2 at2
0 = vit + 1/2 at2
-vit = 1/2 at2 <- divide both sides by "t"
-vi = 1/2 at <- solve for "t"
t = -2vi / a
= -2(13) / -9.81
t = 2.6 sThe answer for time using this method doesn’t have to be doubled, since it is already for the entire flight.
- It is slightly different from the answer we got using the first method (2.7s), but that sort of a difference isn’t important. It is just because of slightly different methods of number crunching.